
This is a vector:

A vector has a magnitude (size) and direction:
The length of the line shows its magnitude and the arrowhead points in the direction.
We can add two vectors by joining them head-to-tail:
And it doesn’t matter which order we add them, we get the same result:
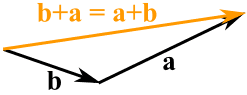
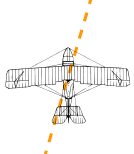
Example: A plane is flying along, pointing North, but there is a wind coming from the North-West.
The two vectors (the velocity caused by the propeller, and the velocity of the wind) result in a slightly slower ground speed heading a little East of North.
If you watched the plane from the ground it would seem to be slipping sideways a little.
Have you ever seen that happen? Maybe you have seen birds struggling against a strong wind that seems to fly sideways. Vectors help explain that.
Velocity, acceleration, force and many other things are vectors.
Subtracting
We can also subtract one vector from another:
- first, we reverse the direction of the vector we want to subtract,
- then add them as usual:
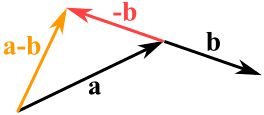
a − b
Notation
A vector is often written in bold, like a or b.
| A vector can also be written as the letters of its head and tail with an arrow above it, like this: |
 |
Calculations
Now … how do we do the calculations?
The most common way is to first break up vectors into x and y parts, like this:
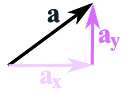
The vector a is broken up into
the two vectors ax and ay
Adding Vectors
We can then add vectors by adding the x parts and adding the y parts:
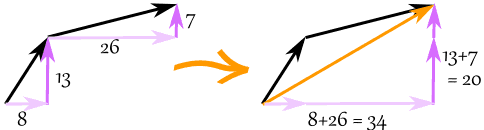
The vector (8,13) and the vector (26,7) add up to the vector (34,20)
Example: add the vectors a = (8,13) and b = (26,7)
c = a + b
c = (8,13) + (26,7) = (8+26,13+7) = (34,20)
When we break up a vector like that, each part is called a component.
Subtracting Vectors
To subtract, first reverse the vector we want to subtract, then add.
Example: subtract k = (4,5) from v = (12,2)
a = v + −k
a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)
Magnitude of a Vector
The magnitude of a vector is shown by two vertical bars on either side of the vector:
|a|
OR it can be written with double vertical bars (so as not to confuse it with absolute value):
||a||
We use Pythagoras’ theorem to calculate it:
|a| = √( x2 + y2 )
Example: what is the magnitude of the vector b = (6,8) ?
|b| = √( 62 + 82 ) = √( 36+64 ) = √100 = 10
A vector with magnitude 1 is called a Unit Vector.
Vector vs Scalar
A scalar has a magnitude (size) only.
Scalar: just a number (like 7 or −0.32) … definitely not a vector.
A vector has magnitude and direction and is often written in bold, so we know it is not a scalar:
- so c is a vector, it has magnitude and direction
- but c is just a value, like 3 or 12.4



